-AA+A
TUDO QUE VOCÊ PRECISAVA SABER SOBRE LIMITES - UM RESUMO
Faça o download desse material em pdf clicando aqui!
1. Definição de limites
Imagine o seguinte exemplo: uma formiga está tentando chegar no ponto em x = 3 andando pela curva definida pela função f(x)=x², então, quando chegar, y será 9!
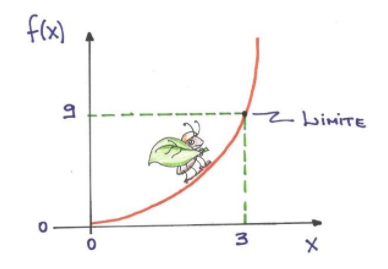
De modo geral, se f(x) é uma função qualquer, então
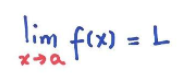
A equação acima pode ser lida como “o limite de f(x) quando x aproxima-se de a é L.” Isso significa que se nós escolhermos valores de x próximos, mas não iguais a a, então f(x) será próximo de L. Além disso, f(x) se aproxima cada vez mais de L, enquanto x se aproxima de a.
A seguinte notação alternativa pode ser usada:
2. Substituição de números para encontrar o limite
Esse seria o primeiro passo para determinar um limite. Nesse caso, basta substituir o valor do limite diretamente na fórmula.
Dado o limite:
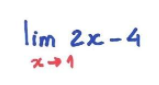
Para resolvê-lo, basta substituir o valor de 1 em x. Logo:
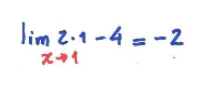
3. Limites indeterminados
As indeterminações podem surgir quando não temos como calcular um limite de maneira racional. Por exemplo:
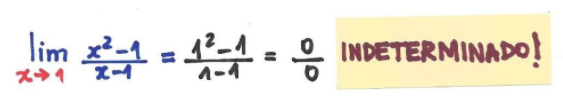
0/0 é um problema! Nós realmente não sabemos o valor de 0/0 (é "indeterminado"), então precisamos de outra maneira para encontrá-lo. Então, em vez de tentar trabalhar para x = 1 vamos tentar aproximar cada vez mais os valores:
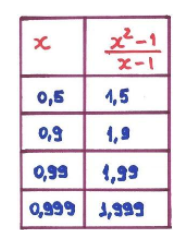
É possível notar que quando x se aproxima de 1, então (x²-1) (x-1) se aproxima de 2. Estamos, agora, diante de uma situação interessante:
- Quando x=1 não sabemos a resposta (a função é indeterminada);
- Mas podemos ver que o limite é dois, pois quanto mais próximo de 1 x está, mais próximo de 2 é o valor da função.
4. Limites tendendo ao infinito
Vamos começar com um exemplo interessante: pergunta-se qual o valor de 1/∞. Resposta: não sabemos! E por que não sabemos? A razão mais simples é que o infinito não é um número, e sim uma ideia. Talvez pudéssemos dizer que 1/∞ = 0, ... mas isso também seria um problema, porque se dividirmos 1 em pedaços infinitos, eles terminam em 0 cada e se somarmos novamente, o resultado será 0 e não 1. O que aconteceu com o 1?
Em vez de dizer que x se aproxima de algum número finito, pode-se dizer que x se tornar cada vez maior e perguntar o que acontece com f(x). Se houver um número L tal que f(x) chega arbitrariamente perto de L, se alguém escolher um x suficientemente grande, então escrevemos:
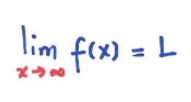
Lê-se: o limite da função f(x) para x tendendo ao infinito é L.
Exemplo:
Em vez de tentar achar o valor no infinito (porque não podemos obter uma resposta sensata), vamos tentar valores cada vez maiores de x:
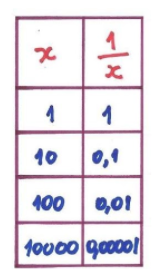
Agora podemos ver que quando x fica maior, 1/x tende para 0. Estamos diante de uma situação interessante: não podemos dizer o que acontece quando x chega ao infinito, mas podemos ver que 1/x se aproxima de 0.
O gráfico comporta-se da seguinte maneira:
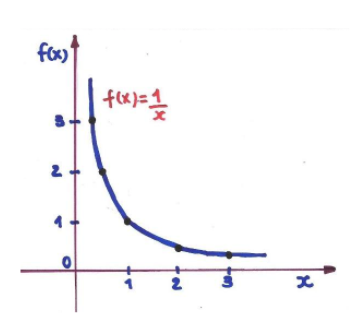
Se colocarmos o x tendendo a zero, vemos que o limite é indeterminado. E, de acordo com as observações no gráfico, ele está tendendo ao infinito.
5. Limites laterais
Sobre uma função f(x) com uma "quebra", assim:
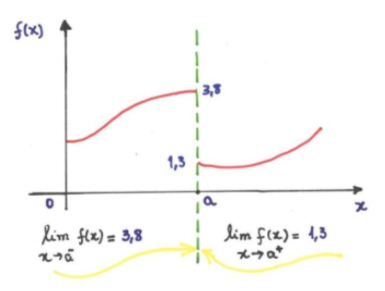
O limite não existe em "a". Não podemos dizer qual é o valor em "a" porque há duas respostas concorrentes:
3,8, quando nos aproximamos do ponto pela esquerda e
1,3 quando nos aproximamos do ponto pela direita.
Nesses casos, podemos usar os sinais especiais "-" ou "+" (conforme gráfico acima) para definir limites unilaterais:
O limite à esquerda (-) é 3,8
O limite à direita (+) é de 1,3
E o limite ordinário (bilateral) "não existe"
6. Propriedades de Limites
Limite de uma constante
Se a e c são constantes, então:
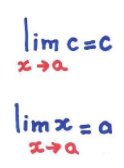
Limite da soma, produto e quociente
Seja F1 e F2 duas funções dadas no qual os limites de x→a são conhecidos,
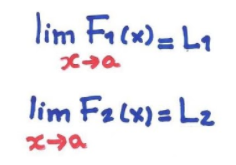
Então,
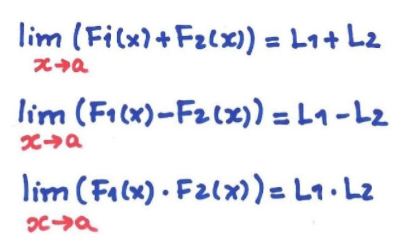
E, por fim, se
, então
, então
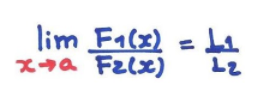
7. Quando limites não existem
Isso pode realmente acontecer e, nessa seção, veremos alguns exemplos de limites que não existem. Primeiro, vamos concordar sobre o que chamaremos de limite não existente.
Definição: Se não há nenhum valor para L no limite:
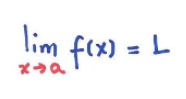
Então, nós dizemos que o limite não existe.
Exemplo: Função sinal próximo a zero, x=0. A função sinal é definida como
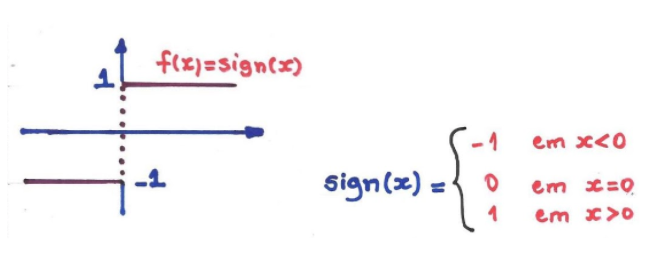
Nota-se que o sinal de zero é definido em zero. Entretanto, a função não tem limite em x=0. Suponha um número L qualquer, então:
Portanto, uma vez que pegarmos um pequeno número positivo de x, L=+1, mas se pegarmos um pequeno número negativo de x, L= -1. O problema está que L não pode ser +1 e -1 ao mesmo tempo.
8. Teorema do Confronto
Suponha que:
e
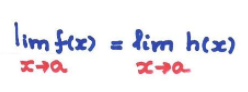
Então:
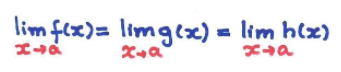
9. Limites trigonométricos
Há dois limites fundamentais: o limite do seno e o limite do cosseno.
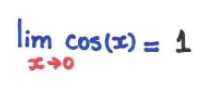
10. Exemplos de limite
Substituição: a primeira tentativa é apenas colocar o valor do limite e verificar se funciona (em outras palavras, substituição).
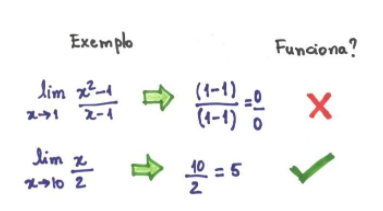
Fatorização: é possível tentar a decomposição dos elementos.
Conjugados: Quando for uma fração, multiplicar a parte superior e inferior por um conjugado também pode ajudar.
11. Regra de L´Hópital
É uma regra para limites tendendo ao infinito a fim de sair da indeterminação. Para ter um bom entendimento, observe o exemplo a seguir:
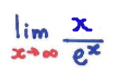
Há uma indeterminação no limite acima. Então, separamos a função em duas novas funções, sendo:
Logo, para calcular o limite, tira-se a derivada de f(x) e g(x), ficando:
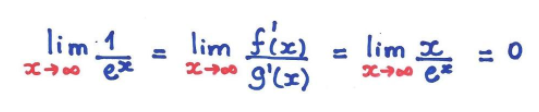
Você precisa de uma conta no Me Salva! para acessar os conteúdos.