Faça o download desse resumo em pdf clicando aqui!
TUDO QUE VOCÊ PRECISAVA SABER SOBRE LIMITES - UM RESUMO
O que é um limite?
Imagine uma formiga está tentando chegar no ponto em x = 3 andando pela curva definida pela função f(x)=x². Quando ela chegar, f(x) = 9! Esse é o limite da função para x tendendo a 3.
Limites indeterminados
O limite é indeterminado se o resultado do limite, somente substituindo o valor na função, não resulta em um número real.
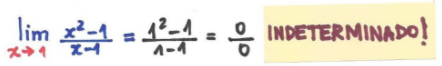
NOTA MENTAL: A indeterminação acontece sempre que há alguma operação envolvendo o infinito! Infinito não é um número, é uma “ideia”! |
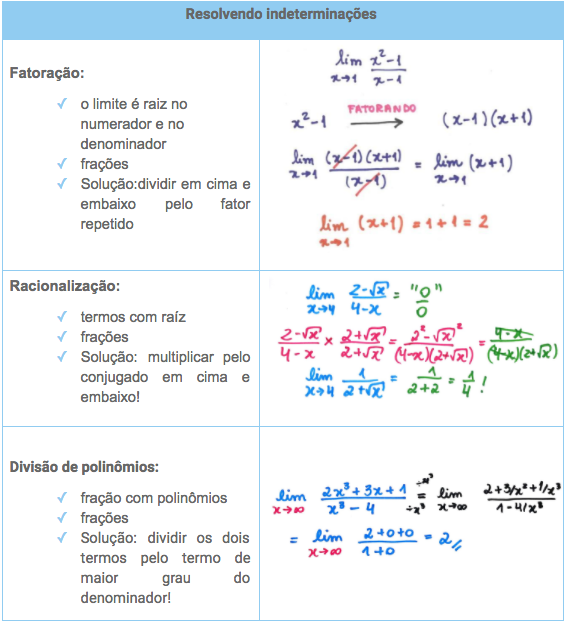
Para resolver estes limites, devemos usar alguma artimanha matemática:
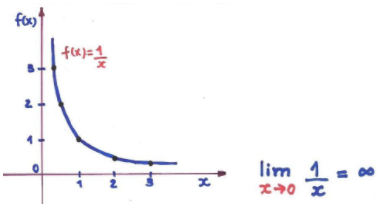
A divisão de infinitos é indeterminada… mas se quisermos passar a ideia de que uma função tende a um valor muito, muito grande (ou a um valor muito pequeno), podemos dizer que o limite dela é infinito!
Limites laterais
Sobre uma função f(x) com uma "quebra", assim:
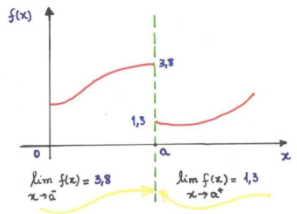
O limite à esquerda (-) é 3,8
O limite à direita (+) é de 1,3
Logo, a função acima é descontínua, pois os limites pelos lados são diferentes! Quando isso acontece, o limite ordinário "não existe"!
Propriedades de Limites
Limite de uma constante
Se a e c são constantes, então:
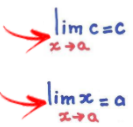
Limites da soma, produto e quociente
Seja F1 e F2 duas funções dadas no qual os limites de x→a sabemos,
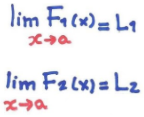
Então:
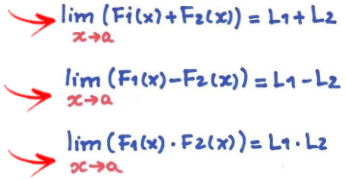
Finalmente, se

Limites não existe?
A função cos(x), por exemplo, fica variando entre -1 e 1. Por isso, se x for muito grande, não se sabe que valor a função cos(x) terá.
NOTA MENTAL: Não ter limite não é a mesma coisa que ter limite indeterminado! O indeterminado só precisa ser guiado para a determinação!
|
Teorema do Confronto
Se uma função g é limitada por outras duas funções (h e f), e 
Então: 
Limites Fundamentais
Alguns limites são muito importantes para não serem citados:
Regra de L’Hópital
SPOILER ALERT! Se você ainda não estudou derivadas, pare por aqui! Se não, bem-vindo à um modo legal de resolver limites!
|
É uma regra para limites tendendo ao infinito a fim de resolver uma indeterminação. Deriva-se as duas funções da fração: