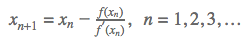Faça o download desse resumo em pdf clicando aqui!
RESUMO DERIVADAS
DEFINIÇÃO
A derivada nada mais é do que a inclinação da reta tangente a y=f(x) ou a taxa de variação instantânea de y em relação a x.
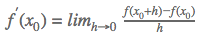
DIFERENCIABILIDADE
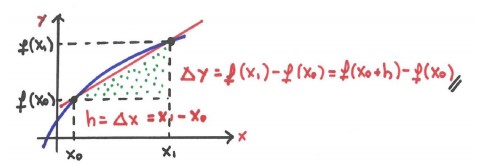
Para a função f(x) ser diferenciável – derivável – em x0 deverá existir o limite:
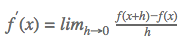
E não esquecer que os limites laterais também devem existir e que devem ser iguais!
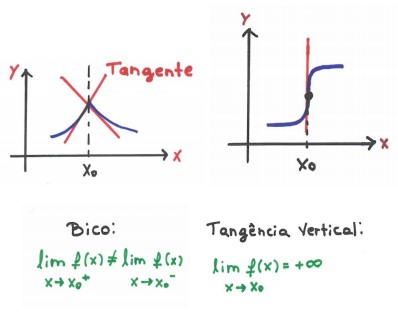
Podemos ter casos em que a função f(x) é contínua em x0, porém não é derivável em x0. Os dois casos mais comuns são o ponto de bico e o ponto de tangência vertical.
TÉCNICAS DE DERIVAÇÃO
Para facilitar o estudo, aí está uma tabela resumo das derivadas mais legais!

REGRAS DE DERIVAÇÃO
Aqui estão aquelas propriedades e regrinhas básicas das derivadas que não podemos esquecer!

REGRA DA CADEIA
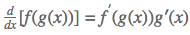
Essa regra já é um pouco mais complicada. Então, segue um exemplo para visualizar melhor como ela funciona.
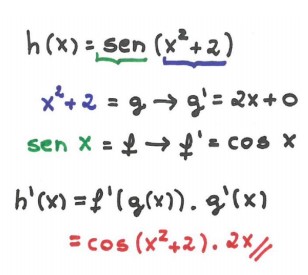
Há outra maneira de fazer a regra da cadeia. Primeiro, identifique quantas funções existem na composição, depois, derive de fora para dentro. Dá uma olhada nos exemplos a seguir e veja se não é mais fácil!

DERIVADA IMPLÍCITA
Usamos a derivação (diferenciação) implícita quando não conseguimos isolar as variáveis. Exemplo:
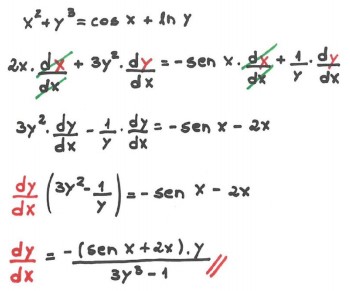
TAXAS RELACIONADAS
Problemas com taxas relacionadas podem ser resolvidos seguindo os seguintes passos.
Passo 1: Detecte cada quantidade que varia com o tempo e outras que possam ser relevantes para a resolução do problema.
Passo 2: Indique as taxas de variação que são conhecidas e a taxa de variação que deve ser encontrada. Analise cada taxa como uma derivada.
Passo 3: Encontre uma relação entre essas variáveis e equacione elas. Para tal, geralmente usamos geometria.
Passo 4: Derive, através da derivação implícita, ambos os lados da equação em relação ao tempo para obter uma relação entre as taxas conhecidas e a taxa desconhecida.
Passo 5: Após o passo 4, substitua os valores conhecidos das taxas e das variáveis e resolva a equação encontrada para a taxa de variação desconhecida.
DERIVADA PRIMEIRA E SEGUNDA
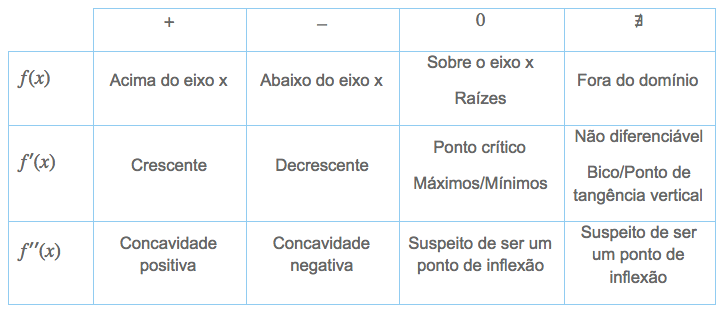
Obs.: O ponto de inflexão ocorre quando a derivada segunda muda de sinal!
ESBOÇO DE GRÁFICOS
Passo 1: Encontrar pontos de interesse de f(x), se possível, como o valor da função quando x=0 e as raízes da função. Podem ser difíceis de encontrar, mas não se atenha, vá para o passo 2!
Passo 2: Encontrar as assíntotas horizontais. Lembrando que para achar as assíntotas horizontais, temos que:
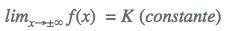
Passo 3: Procurar as assíntotas verticais. Encontramos as nossas assíntotas verticais quando nossa função não existe, por exemplo, divisão por zero e raízes de números negativos.
Passo 4: Buscar pelos máximos e mínimos. Para isso, derivamos a f(x), igualamos a zero e encontramos os pontos críticos, e se analisa o sinal.
Passo 5: Analisar a concavidade. Para tanto, deriva-se duas vezes, encontrando a derivada segunda f’’(x), iguala-se a zero para obter os suspeitos de inflexão e se analisa o sinal.
Passo 6: Traçar o esboço. Para facilitar o teu trabalho, desenhe, abaixo do eixo x, duas linhas, uma para f’(x) e outra para f’’(x), colocando, respectivamente, os pontos críticos e pontos de inflexão, juntamente com as análises de sinais. Dê uma olhada no desenho abaixo!
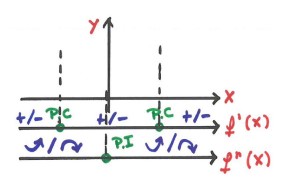
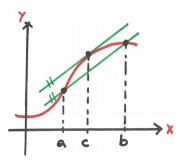
TEOREMA DO VALOR MÉDIO
O teorema diz que, entre dois pontos [a, b] de uma função diferenciável f, há um ponto c no qual a sua derivada f’(c) é a inclinação da reta tangente paralela à reta secante que passa pelos pontos [a, b].
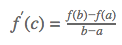
REGRA DE L’HÔPITAL
Aplicamos a regra de L’Hôpital quando o 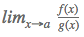 resultar em uma indeterminação do tipo
resultar em uma indeterminação do tipo  . Dessa forma, devemos derivar as funções. Caso ainda resulte em uma indeterminação, deve-se continuar derivando.
. Dessa forma, devemos derivar as funções. Caso ainda resulte em uma indeterminação, deve-se continuar derivando.
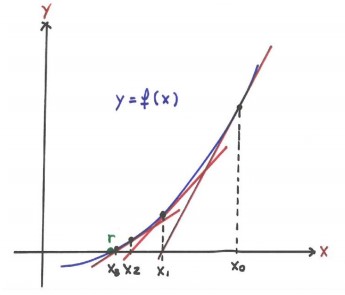
MÉTODO DE NEWTON
Utilizamos este método quando queremos achar um valor aproximado da nossa raiz de uma função f(x). Lembrando que quanto maior o número de interações, mais preciso vai ser o valor de r.